The Mathematics of Poker

A very good book has just gone to press:

The Mathematics of Poker, by Bill Chen and Jerrod Ankenman.

I received a review copy of it and found it to be an informative and challenging read. Short review: This is one of the most important books about poker ever published.  For a longer review you can read Terrence Chan’s great early review of the book.  

Few books on gambling take a truly analytical approach. In fact, the only other book in my library which comes close is The Theory of Gambling and Statistical Logic, Revised Edition, by Richard Epstein. Unfortunately, that book has very little poker poker content. Chen and Ankenmen do the world a service by with their thorough analysis of poker.  Their methodology is clear, the problems and solutions are interesting, and their insights into the game are remarkable.  They’ve also done an excellent job of keeping most of the mathematics accessible to anyone who has a solid grasp of algebra.

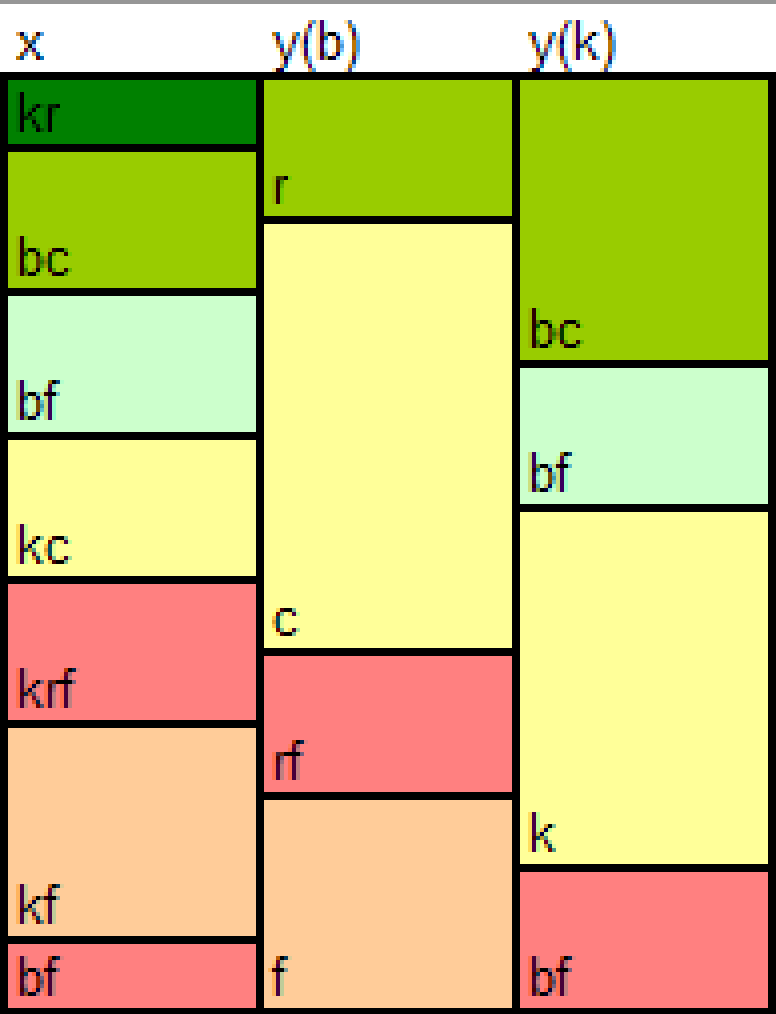
Here is an example of the kinds of insights you can get from reading and understanding this book.  Below is a topological representation of the solution to the one street heads-up finite pot game with a maximum of two bets.

The strongest hands are at the top of the chart, and the weakest hands are at the bottom. The action maps as: f=fold, k=check, c=call, b=bet, r=raise. Each column reprsents the optimal strategy for the game.  The strategy for the first player is in the X column, and the strategy for the second player is in the Y columns. If X bets, then the Y(b) column is used, if X checks, then the Y(k) column is used.  It’s important to note that the actual location of the boundaries are not illustrated here, only their relative ordering.

Some basic insights from the solution: You need a stronger hand to check-raise with than you bet-call with. You should fold some of your value bets. Your bluff raises should be done with hands which are stronger (not weaker) than your bluffs.